Security+ Course – 6.5 Public Key Infrastructure (PKI)

1. Trust Models

Requirements for Symmetric Key Exchange:

• The 2 parties must be confident that they are really communicating with each other and not an imposter
• The 2 parties must be confident that nobody is eavesdropping on the key exchange

Asymmetric Cryptography

• Users don’t need to share their private keys
• Users can share their public keys freely
• Eavesdropping protection isn’t needed during the key exchange

We still need to prevent imposters. How do you know that the person sending us their public key really is who they claim to be?
There are three basic ways that we can obtain this assurance.

• In person key exchange
• Web of Trust (WOT)
• Public Key Infrastructure (PKI)

Web of Trust (WOT)

The Web of Trust was first introduced by Phil Zimmermann with the introduction of his PGP encryption software. The Web of Trust depends upon indirect relationships such as those you would find on LinkedIn. While you might not know the person you wish to communicate with personally, you might know somebody who knows that person. Or perhaps you have a third-level connection where you know somebody who knows somebody who knows that person. The Web of Trust takes advantage of this by using digital signatures to vouch for the public keys of individuals. Every participant signs the public keys of everyone they know when they verify that the public key belongs to that person.

WOT Issues

• Decentralised approach makes it difficult to manage
• High barrier to entry for new people
• Requires a good deal of technical knowledge on behalf of each user

For these reasons the WOT never really took off outside of the technical community.

2. Public Key Infrastructure (PKI)

The PKI solves many of the practical issues associated with the web of trust by introducing the concept of certificate authorities. Instead of relying upon the peer-to-peer trust relationships, the public key infrastructure relies upon the trusts that participants have in highly trusted centralised service providers. These providers, known as certificate authorities(CA’s), form the basis of the public key infrastructure.

Certificate Authorities (CA)

Certificate authorities verify the identity of individuals and organisations and then issue those individuals and organisations digital certificates, vouching that the public key associated with that entity actually belongs to them.
The process is similar to what you would do to get a drivers licence:

1. You go to your region’s Department of Motor Vehicles and you’re asked to prove your identity through a fairly rigorous process. This likely includes providing several forms of identification and proof of residence
2. Once the DMV verifies your identify, they issue you a certificate. In this case, your driver’s license is a plastic certificate. It includes information about you that the DMV verified as true as well as a photograph
3. You now have a certificate to prove your identity to someone else. You can simply show them your driver’s license
4. If the individual seeing your driver’s license trusts the DMV, they can simply verify your license as authentic and check that you match the photo on the license. They then have confidence knowing that you’ve already proven your identity to the DMV.

Digital certificates are the identity card of the digital world

Obtaining a digital certificate

1. You approach a certificate authority
2. The CA will ask you to prove your identity. This may simply involve verifying ownership of a domain name or may be more rigorous and involve physical proof of identity depending upon the type of certificate that you are trying to obtain
3. If the CA is satisfied that you are who you claim to be, you then provide the CA with your public encryption key over a secure channel
4. The CA uses this information to create a digital certificate that contains information about your identity and your public key. The certificate is digitally signed by the certificate authority
5. You can then provide your digital certificate to anyone you’d like to communicate with. You don’t have to worry about sending the certificate securely because it doesn’t contain any sensitive information
6. The person receiving the certificate does not have to verify your identity directly. They simply verify that the certificate is valid by verifying the CAs signature on the certificate
7. Assuming they trust the CA, the person may then confidently use that public key to encrypt messages for you

3. Hash Functions

A hash function is a one-way function that transforms a variable length input into a unique, fixed-length output.

One Way Functions: cant be reversed. If you have content, you can use a hash function to calculate the hash value of that content, but you can’t go the other way around. If you have a hash value, you can’t use it to figure out the original content unless you already have a copy of that text.
Variable length input into fixed length output: That simply means that you can send input of any length to a hash function, and the hashes that it produces will always be the same length. Input 2 words or an entire book, and the output will be the same length.
Unique output: Hash functions produce unique output. You should not be able to find two different inputs that produce the same hash value as output.

For a hash function to be effective, it must meet all of the criteria above

How Hash Functions May Fail

1. If they are reversible: you don’t want any way for someone seeing the hash value to determine the content of the message
2. It is not collision resistant: This means that it doesn’t achieve the unique output part of the definition, and that it is possible to find two inputs that produce the same hash output. If that were the case, it makes it possible to forge digital signatures and digital certificates, and that’s clearly undesirable

Common Hash Functions

EXAM TIP: you should be familiar with these hash functions

Message Digest 5 (MD5)

• Invented by Ron Rivest in 1991
• MD5 is the fifth in a series of hash functions. MD5 replaced the MD4 algorithm after research showed that MD4 was insecure
• Message digest is another term for hash
• MD5 produces 128 bit hash
• MD5 is no longer secure

Secure Hash Algorithm (SHA)

Created by NIST as a government standard

SHA-1:
– Produces a 160 bit hash value
– Contains security flaws and is no longer considered secure

SHA-2:
– Is a family of six has functions
– Produces an output of 224, 256, 384 and 512 bits
– Uses a similar mathematical approach to SHA-1 and MD5. This represents a future risk to SHA-2

SHA-3:
– Designed as an eventual replacement of SHA-2
– Uses a completely different mathematical approach than SHA-2
– Produces hashes of user selected fixed length.

Race Integrity Primitives Evaluation Message Digest (RIPEMD)

Some academic researchers do not trust the SHA algorithms because of their origins within the US government, and specifically the involvement of the National Security Agency in the creation of the SHA-1 and SHA-2 algorithms. A group of Belgian researchers developed an alternative known as RIPEMD.

• Produces 128, 160, 256, 320 bit hashes
• 128 bit version is no longer considered secure but the rest are

Calculating a Hash

There are websites available that will allow you to calculate a hash online. An example of one of these is: https://xorbin.com/tools/sha256-hash-calculator

Hash-Based Message Authentication Code (HMAC)

HMAC combines symmetric cryptography with hashes to provide authentication and integrity for messages. When using HMAC, the sender of a message provides a secret key that is used in conjunction with the hash function to create a message authentication code. The recipient of the message can then repeat the process with the same secret key to verify the authenticity and integrity of the message.

4. Digital Signatures

Digital signatures provide an electronic counterpart to physical signatures. Digital signatures use asymmetric cryptography to achieve the goals of integrity, authentication and non-repudiation.

What Signed Message Recipients Know

1. Authentication: the person owning the public key used to sign the message is actually the person who created the message
2. Integrity: the message was not altered after being signed
3. Non-repudiation: the recipient could prove these facts to a third party

Digital Signatures Depend on

1. Collision resistant hash functions (any 2 inputs wont produce the same output)
2. Asymmetric cryptography: anything encrypted with one key from an asymmetric key pair, may only be decrypted with the other key from that same pair.

Encrypting a Digital Signature

In other areas of encryption you use public keys to encrypt data and private keys to decrypt them. That’s because we were trying to create messages that only someone with a private key could read. In the case of digital signatures, we reverse this, and use the private key for encryption and the public key for decryption. That’s because our goal is different. We don’t want to create a secret message, but rather we want to create a message that could only have been created by a specific person who possesses the private key and can then be verified by anyone with a corresponding public key.

Digital Signature Example: Alice wants to send a message to Bob that includes Alice’s digital signature

1. Alice creates a hash of the message
2. Alice then encrypts that hash value using her private key. This is the digital signature
3. Alice then sends both the message and the digital signature to Bob
4. When Bob receives the message he takes the message and computes it using the same hash function that Alice did. As they are using the same hash function they will get the same output
5. Bob then takes the digital signature from that message and decrypts it using Alice’s public key. This will give him the hash value Alice created in step 2
6. Bob compares the hash values he created in step 4 and the hash value he got in step 5. If they are the same, Bob knows that Alice created this message, because only Alice could have encrypted the message digest with her private key. If someone else had created the digital signature with a different private key, Bob would still have tried to decrypt it with Alice’s public key. He wouldn’t get the correct result if he did this, and he would reject the message because the two values didn’t match
7. Bob also knows that nobody altered the message after Alice created it, because that would have changed the hash value that Bob computed himself
8. Bob can prove all of this information to a third party, Charlie, by having Charlie repeat the signature verification process himself

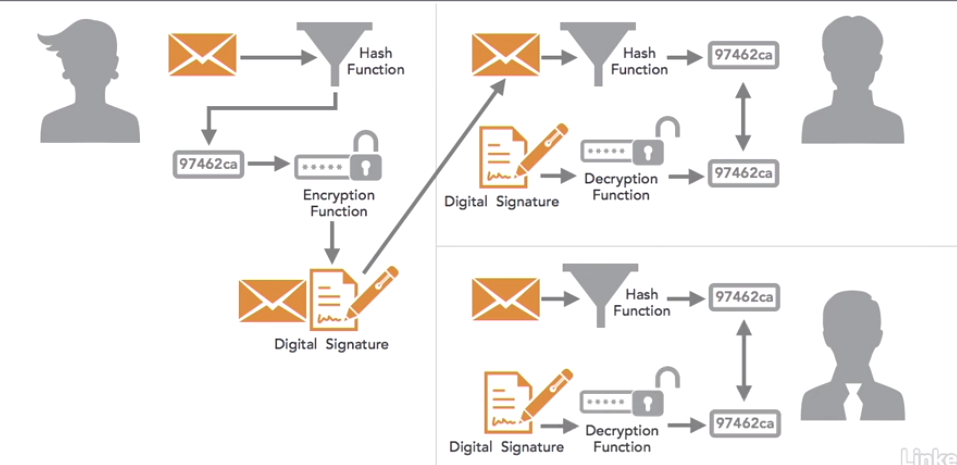
Important Note: digitally signing messages does not provide confidentiality. In the example above, anyone could read the message, not just Bob. If Alice wanted to be sure that only Bob could read the message, she could take the added step of encrypting the message with Bob’s public key.

5. Digital Signature Standard

The Digital Signature Standard is a US Federal government standard for appropriate digital signature algorithms and is published by the National Institute for Standards in Technologist, NIST. The current version of the standard came out in 2013. It’s published as a Federal Information Processing Standard or FIPS number 186-4. It is a 100 plus page document.

Approved DSS Algorithms

The Digital Signature Standard supports three different digital signature algorithms for use in the US government.

1. Digital Signature Algorithm (DSA): this is described within FIPS 186-4 and is very closely related to the ElGamal cryptographic algorithm
2. Rivest, Shamir, Adelman (RSA): The Digital Signature Standard endorses the uses of RSA for digital signatures that are described in American National Standard X9.31 and Public Key Cryptography Standard, or PKCS number one
3. Elliptic Curve Digital Signature Algorithm (ECDSA): The Digital Signature Standard endorses the use of ECDSA for digital signatures as described in American National Standard X9.62.

All three of these algorithms are considered secure and acceptable for use in creating and verifying digital signatures.

6. Creating A Digital Certificate

The process for creating digital certificates follows the X.509 standard created by the International Telecommunications Union, or ITU. You might hear digital certificates referred to as X.509 certificates.

Example of creating a certificate

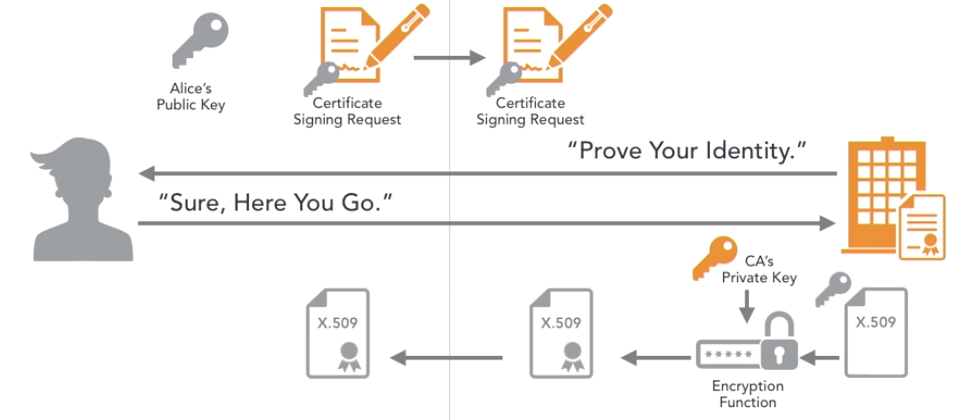
1. Alice first creates a public private key pair for the encryption algorithm of her choice
2. She then creates a message called a certificate signing request, or CSR. The CSR contains Alice’s public key as well as Alice’s name and other identifying information such as an email address or a server name
3. Alice then sends the CSR to the certificate authority of her choice. This might be an independent organisation that is trusted by many people around the world, or it may be a private certificate authority operated for use within her organisation
4. The CA takes whatever action is necessary to validate the identity of the requester. It is the CA’s responsibility to perform sufficient identity verification to put it’s own seal of approval on the certificate. This is in the CA’s best interest because if a CA starts issuing invalid certificates, people will stop trusting that CA
5. Once the CA is satisfied that the sender is legitimate, it removes the public key from the certificate signing request and places it in the format of an X.509 certificate
6. The CA then uses it’s private key to place the CA’s digital signature on the digital certificate
7. The CA sends the certificate back to the requester
8. The requester may then use that certificate and provide it to anyone who wishes to communicate with them. A third party wishing to communicate with Alice can then verify that the certificate is valid by simply checking that the CA’s digital signature on the certificate is valid
9. If the signature is correct, the third parties know that they can use the public key contained in the certificate to communicate with the person named on the certificate, Alice

Generating a CSR

This example is on A Linux system using openssl:

1. Use the command to generate the request with a 2048 bit key: openssl -new -newkey rsa:2048
2. It creates a private key and calls it ‘privkey.pem’
3. It then asks for a password to associate with the private key
4. It then asks for verification information such as: country, email, organisation etc…
5. It then displays the request in the following format:
   
6. This request contains the public key that it just generated as part of that RSA key pair as well as all of the identifying information necessary to create the digital certificate. You could provide this request then to any certificate authority of your choice who would then verify your identity and then use this information to create the digital certificate that contains the public key.

7. Revoking a Digital Certificate

The security of digital certificates depends upon the security of the private key associated with that certificate. If the certificate owner’s private key is compromised, the owner needs a way to revoke the digital certificate so that it can’t be used to impersonate the owner later on.

2 Methods of revoking a certificate

Both methods are maintained by the certificate authority who issued the certificate

1. Certificate revocation List (CRL): this is a list the CA provides with the serial numbers of revoked certificates. Anyone accessing a digital certificate is responsible for download the CRL and verifying that the serial number is not included on that list before relying upon the public key contained within the certificate. This approach was inefficient because it often had time delays and consumed a lot of network bandwidth as everyone on the internet attempted to download CRLs everyday from every certificate authority and the lists themselves grew longer
2. Online Certificate Status Protocol (OCSP): In this approach, anyone about to rely upon a public key contained within a digital certificate sends a request to the CA to verify that the certificate is still valid. The CA then checks the serial number of the certificate against its list of revoked certificates and sends back a yes or no response.Most modern web browsers rely upon OCSP for determining certificate validity. One exception to this is Google Chrome, which uses Google’s own proprietary approach for verifying certificates.

8. Certificate Stapling

The primary issue with OCSP is that it places a significant processing burden on the OCSP servers operated by certificate authorities. These servers must process requests from every single visitor to a website or other user of a digital certificate verifying that the certificate is valid and hasn’t been revoked. Certificate stapling is an extension to OCSP that minimises the burden on the certificate authority’s OCSP servers.

How Certificate Stapling Works

In the traditional OCPS protocol, when a user visits a website and initiates a secure connection, the website sends its certificate to the end user who would normally then be responsible for contacting the OCSP server to verify the certificate’s validity.

In Certificate Stapling, the web server contacts the OCSP server itself and receives a signed and time stamped response from the OCSP server, which it then attaches or staples to the digital certificate. When the web server receives a request from an end user, it then sends that user the certificate with the stapled OCSP response. The user’s browser then verifies that the certificate is authentic and also validates that the stapled OCSP response is genuine and recent.

Because the certificate authority signed the OCSP response, the user knows that it is from the certificate authority, and the time stamp provides the user with assurance that the CA recently validated the certificate.

The web server can reuse these stapled certificate for the next users that visit the site. This is where the savings dome in the burden on the CA OCSP servers. Often these stapled certificates will be valid for 24 hours

OCSP certificate stapling became widely supported by web browsers in 2014 and 2015.

9. Certificate Authorities

In most cases, organisations choose to use a well-known certificate authority because the vast majority of users around the world will already be configured to trust that certificate authority. However, when you purchase a certificate from a CA, you must pay them a fee. Because of this, organisations sometimes take steps to reduce the number of certificates that they purchase. One way to do this is with self-signed certificates.

These certificates aren’t trusted by the outside world because they’re not signed by a trusted certificate authority, but they can be used for internal purposes. They configure systems throughout the organisation to trust the internal CA. They can then use this internal CA to issue their own certificates for free for internal websites and other uses.

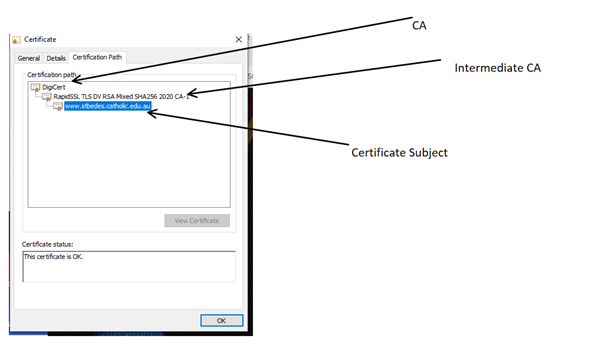
Certificate Chaining

Some organisations go a step further and have their own internal CA trusted by a third-party CA using a technique known as certificate chaining. This allows the organisation to issue their own certificates that are then trusted by external users because the CA that issued them, the organisation’s CA, is trusted by a third-party CA. That’s the chain of trust. In this case, the internal CA is known as an intermediate CA.

Offline CA’s

Another reason to use certificate chaining is to allow the use of offline certificate authorities. The root certificate of a CA is a very sensitive object. Therefore, the private key associated with a certificate is normally not kept on a system that is connected to a network. Instead, it is stored in an offline CA that is only used to sign the certificates of online intermediate CAs belonging to the same organisation. These online CAs are then used to actually issue certificates to customers.

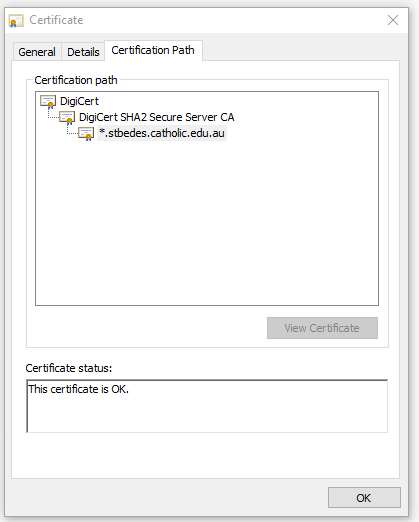
In the following certificate you can see that the Intermediate CA is DigiCert, but the Root CA is also DigiCert. This means that the Root CA DigiCert is probably offline. This reduces the possibility of the Root CA server being hacked.

10. Certificate subjects

The certificate subject is the entity that owns the public key contained within a certificate. By issuing a digital certificate, the certificate authority is certifying that it has verified the identity of the certificate subject and is vouching for the fact that the public key does indeed belong to that entity.

You can view the trusted certificates on your computer and look at the Object Identifiers (OIDs) or properties. These contain things like: Subject, Signature Algorithms, Public key algorithms, extensions etc….

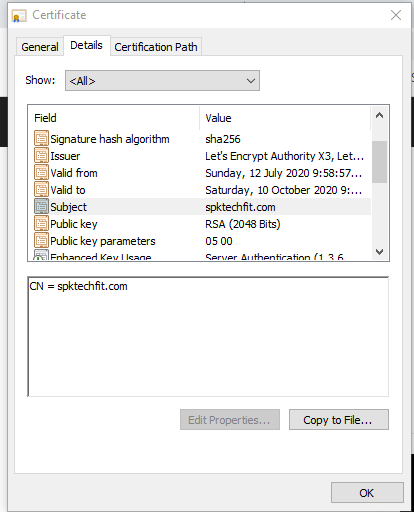
EXAM TIP: you may get questions that ask OIDs. Be sure that you recognise what they are.

Certificate Subjects

– Servers: web, SSH, file, mail etc…
– Devices: SANs, routers, switches, VPNs, access points
– Individuals: names, email addresses
In each of these cases, the purpose of the digital certificate remains the same, to securely associate a public key with an entity, be it a server, an individual or a device.

Certificate Pinning

Certificate pinning is a technology that tells users of certificates that they should not expect a certificate to change over time. When a user receives a certificate from a certificate subject, they’re also told to remember or pin that certificate for an extended period and report any changes to the certificate as a potential security issue.

11. Certificate Types

Root Certificates

These are the core certificates at the heart of a certificate authority, and are used as the very first certificate or the root of trust in chain certificates

Wildcard Certificates

These match a domain and can cover many different subjects. Therefore they should be carefully secured. You can recognise a wildcard certificate by the asterisk * in the name. EG: *.linkedin.com
The asterisk indicates that the certificate may be used for any subject name ending in linkedin.com.

NB: wildcard certificates only go one level deep.
The wildcard replaces a single name, not multiple levels of names. For example, this *.linkedin.com wildcard certificate could not be used for www.secure.linkedin.com, because that’s two levels of depth.

Certificates by Verification Type

There are actually three different types of verification that may be used, and the CA issues different certificates depending upon the degree of identity verification that they performed.

1. Domain Validation (DV): these are the lowest level of trust. To verify this the CA simply checks the ownership of a domain
2. Organisation Validation (OV): This goes a step further. The CA verifies not only that the certificate’s subject owns the domain, but also that the name of the organisation purchasing the certificate is valid. This is done by checking business records, such as state business registrations or reputable business databases
3. Extended Validation (EV): these are the highest level of trust. The CA performs an extensive investigation to verify the physical existence and legitimacy of the organisation

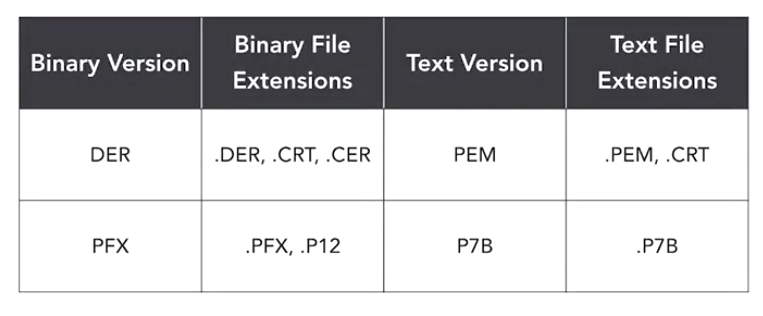
12. Certificate Formats

Digital certificates come in a wide variety of different formats, both binary and text based.

Distinguished Encoding Rules (DER)

• This is the most common format
• Binary format
• Uses .DER, .CRT and .CER extensions

Privacy Enhanced Mail (PEM)

The name comes from an older email standard that is no longer used. But certificated format from that standard is still used today.

• ASCII text equivalent of DER certificates
• You can easily convert between binary DER certificates and text based PEM certificates using tools like OpenSSL
• Uses .PEM and .CRT extensions

EXAM TIP: .CRT files may be either DER binary certificates or PEM text certificates

Personal Information Exchange (PFX)

• Binary format
• Commonly used by Windows systems
• Uses .PFX and .P12 file extensions

P7B Format

• This is the ASCII equivalent of PFX certificates
• Commonly used by Windows systems
• Uses .P7B file extension

Summary Table of Certificate Types

This table contains all information about certificates you need to know for the exam-